2021/04/17
2024-07-21 终极简单的 r13y
这题是 33. 搜索旋转排序数组 的升级版,思路仍然是先找旋转排序数组的最小值在哪里(拐点),也就是153. 寻找旋转排序数组中的最小值
只不过需要防御一手首尾相等,导致无法开始二分。
class Solution {
public boolean search(int[] nums, int target) {
int l = 0, r = nums.length;
// 仅仅需要防御一手由于首尾相等导致无法寻找拐点
while (l < nums.length && nums[l] == nums[nums.length - 1]) {
l++;
}
while (l < r) {
int mid = l + (r - l) / 2;
if (nums[mid] <= nums[nums.length - 1]) {
r = mid;
} else {
l = mid + 1;
}
}
if (target == nums[nums.length - 1])
return true;
else if (target < nums[nums.length - 1])
return binSearch(nums, l, nums.length, target) != -1;
else
return binSearch(nums, 0, l, target) != -1;
}
public int binSearch(int[] nums, int i, int j, int target) {
int l = i, r = j;
while (l < r) {
int mid = l + (r - l) / 2;
if (nums[mid] >= target) {
r = mid;
} else {
l = mid + 1;
}
}
if (l == j)
return -1;
return nums[l] == target ? l : -1;
}
}
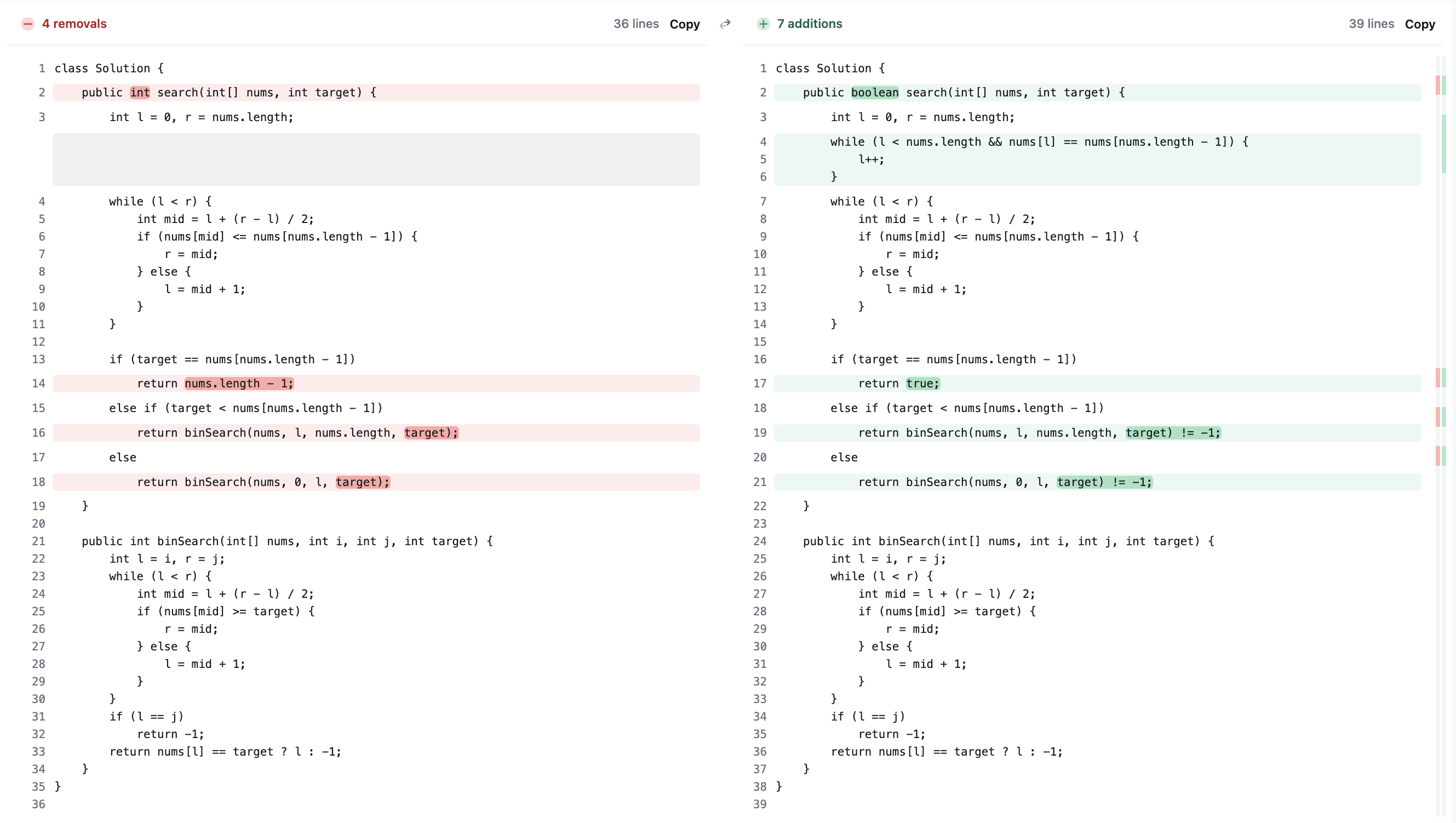
与 33. 搜索旋转排序数组 的区别如下
2021-04-17 二分模板做法
这道题是第33题的带重复元素版本,在第33题的二分模板法基础上,在二分进行的过程中进行一些预处理,使得 check 函数仍然可以正常工作。第154题 也用到了这个思路。
impl Solution {
fn check(l: usize, r: usize, mid: usize, nums: &Vec<i32>, target: i32) -> bool {
if nums[l] < nums[r] {
return nums[mid] >= target;
} else {
if nums[l] <= target && target <= nums[mid] { return true; }
if target <= nums[mid] && nums[mid] <= nums[r] { return true; }
if nums[mid] <= nums[r] && nums[l] <= target { return true; }
return false;
}
}
pub fn search(nums: Vec<i32>, target: i32) -> bool {
let mut l = 0;
let mut r = nums.len() - 1;
while l < r {
unsafe {
while l < r && nums[l] == nums[r] {
l += 1;
}
if l == r {
return nums[l] == target;
}
}
let mid = l + (r - l) / 2;
if Solution::check(l, r, mid, &nums, target) {
r = mid;
} else {
l = mid + 1;
}
}
return nums[l] == target;
}
}
class Solution {
boolean check(int l, int r, int mid, int[] nums, int target) {
if (nums[l] <= nums[r]) { // 已经在递增区间了,很好判断 mid 在 target 的左边还是右边。
return nums[mid] >= target;
} else { // 区间仍然是旋转数组,mid 和 target 的位置有六种情况,其中三种满足 mid 在 target 的右边。
// mid 和 target 都在左上方,且 mid 在 target 的右边
if (nums[l] <= target && target <= nums[mid]) return true;
// mid 和 target 都在右下方,且 mid 在 target 的右边
if (target <= nums[mid] && nums[mid] <= nums[r]) return true;
// mid 在右下方,target 在左上方,且 mid 在 target 的右边
if (nums[mid] <= nums[r] && nums[l] <= target) return true;
return false;
}
}
public boolean search(int[] nums, int target) {
int l = 0, r = nums.length - 1;
while (l < r) {
int mid = l + (r - l) / 2;
// begin fix
if (nums[mid] == target) {
return true;
}
// 转化成可以 check 的问题
while (l < r && nums[l] == nums[r]) {
l++;
}
// end fix
if (check(l, r, mid, nums, target)) {
r = mid;
} else {
l = mid + 1;
}
}
return nums[l] == target;
}
}
2021-01-21 第一次做
class Solution {
public boolean search(int[] nums, int target) {
return search(nums, target, 0, nums.length - 1);
}
public boolean search(int[] nums, int target, int i, int j) {
if (i > j) return false;
int l = nums[i], r = nums[j];
while (l == r && i < j) {
i += 1;
l = nums[i];
}
// 此时要么 l != r 了,要么 i == j 了
// 这个时候就是 33 题了
int idx = (i + j) / 2;
int n = nums[idx];
if (target == n) return true;
if (target == l) return true;
if (target == r) return true;
// 因为此时 n 的位置已经可以确定了,所以先讨论 n 的位置
if (n > r) { // 如果 n 在上
if (l < target && target < n) {
return search(nums, target, i + 1, idx - 1);
} else {
return search(nums, target, idx + 1, j - 1);
}
} else { // 如果 n 在下
if (n < target && target < r) { // t 在下
return search(nums, target, idx + 1, j - 1);
} else {
return search(nums, target, i + 1, idx - 1);
}
}
}
}