2021/01/20
题目描述
一个升序数组,被切了一刀,分为两个部分,这两部分交换位置从新组合在一起,搜索旋转排序数组中的某个数字
2024-07-21 终极简单的 r13y
先找即旋转排序数组的最小值在哪里(拐点),这是153. 寻找旋转排序数组中的最小值
然后我们根据 target 和 拐点的大小关系,判断在哪个有序区间进行二分搜索,同样的思路可以秒81. 搜索旋转排序数组 II
class Solution {
public int search(int[] nums, int target) {
int l = 0, r = nums.length;
while (l < r) {
int mid = l + (r - l) / 2;
if (nums[mid] <= nums[nums.length - 1]) {
r = mid;
} else {
l = mid + 1;
}
}
if (target == nums[nums.length - 1])
return nums.length - 1;
else if (target < nums[nums.length - 1])
return binSearch(nums, l, nums.length, target);
else
return binSearch(nums, 0, l, target);
}
public int binSearch(int[] nums, int i, int j, int target) {
int l = i, r = j;
while (l < r) {
int mid = l + (r - l) / 2;
if (nums[mid] >= target) {
r = mid;
} else {
l = mid + 1;
}
}
if (l == j)
return -1;
return nums[l] == target ? l : -1;
}
}
运用二分思想的解法
这题考察分类讨论的能力,首先我们画出这个数组的结构:
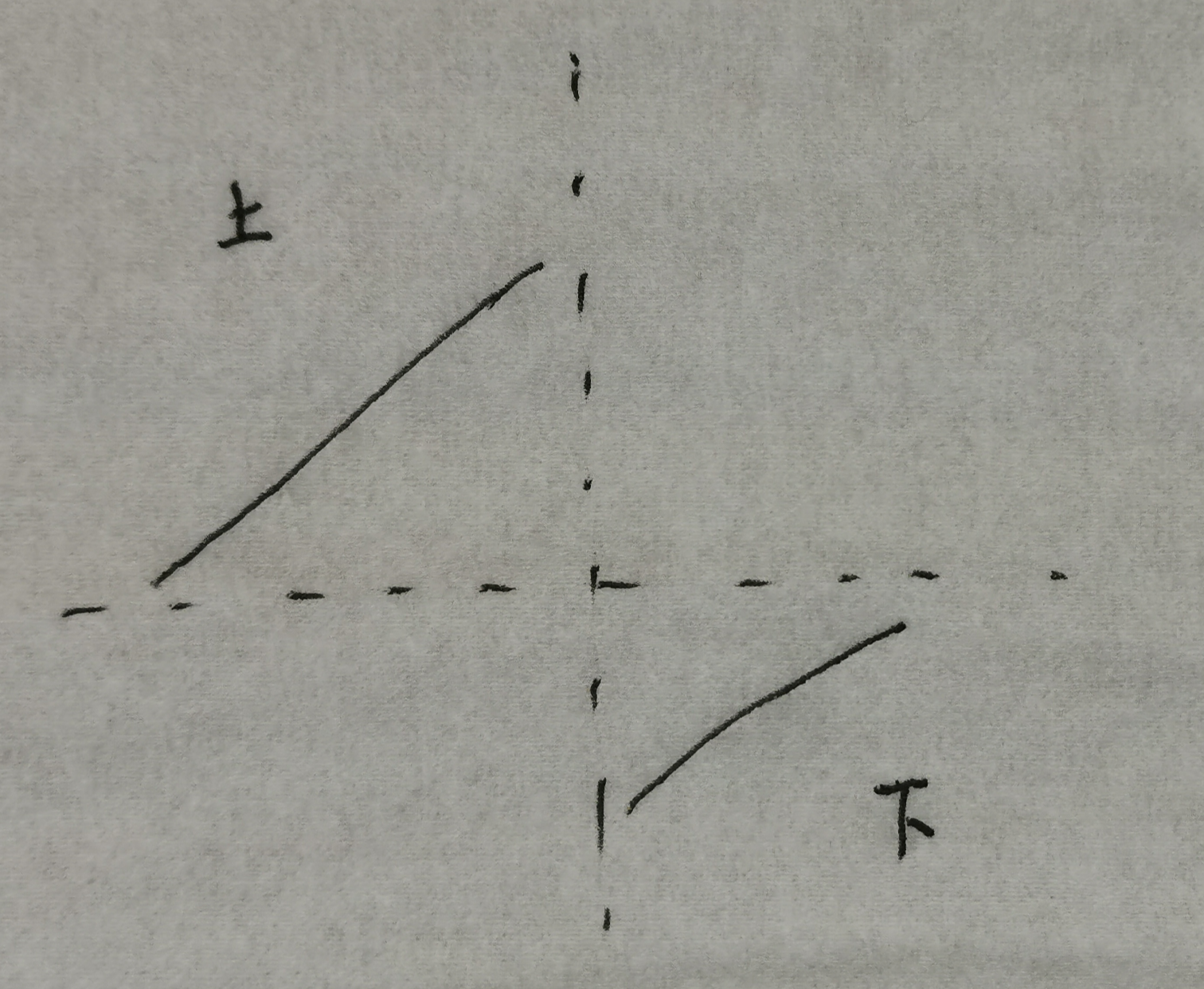
对该数组进行二分查找时,一定可以判断出 mid 的值处于「上」还是「下」,这样我们可以对 mid 进行分类讨论:
- 如果
mid落在「上」:
如果 target 也落在「上」且小于 mid,那么 target 在左半边,否则 target 在右半边 - 如果
mid落在「下」:
如果 target 也落在「下」且大于 mid,那么 target 在右半边,否则 target 在左半边
这里为什么是对 mid 进行分类讨论,而不是对 target 进行分类讨论呢? 原因在于,当我们求出 mid 的值的时候, 就已经可以确定 mid 处于「上」还是「下」了,而 target 仍然处于 「上」、「下」叠加态。 同样的,我们也不会对「拐点」进行分类讨论,因为我们根本都还不知道拐点在哪里。
分类讨论的时候,如果不知道怎么讨论,最好先对已经可以确定的量去讨论
class Solution {
public int search(int[] nums, int target) {
return search(nums, target, 0, nums.length - 1);
}
public int search(int[] nums, int target, int i, int j) {
if (i > j) return -1;
int idx = (i + j) / 2;
int l = nums[i], r = nums[j], n = nums[idx];
if (target == n) return idx;
if (target == l) return i;
if (target == r) return j;
// 因为此时 n 的位置已经可以确定了,所以先讨论 n 的位置
if (n > r) { // 如果 n 在上
if (l < target && target < n) { // target 也在上,并且小于 n
return search(nums, target, i + 1, idx - 1);
} else {
return search(nums, target, idx + 1, j - 1);
}
} else { // 如果 n 在下
if (n < target && target < r) { // target 也在下,并且大于 n
return search(nums, target, idx + 1, j - 1);
} else {
return search(nums, target, i + 1, idx - 1);
}
}
}
}
转化成标准二分问题
我们需要定义一个 f,使得:
- 小于 target 的位置 mid,有 f(mid) = false
- 大于等于 target 的位置 mid,有 f(mid) = true
当我们求出一个 num[mid] 时,我们判断这个 num[mid] 到底是在 target 的左边还是在它的右边。
我们的 f 需要对所有 mid 在 target 右边的情况返回true,否则返回 false,这样 f 一定是单调的,值域是 ffffftttt,满足二分的使用场景。
由于 check 函数也需要引入 [l, r),参数,直接使用 r 会越界,因此先不搜索数组的最后一个元素,只考察[0, len - 2] 范围内的子数组,如果没有搜索到,此时 l 会位于 len-1 处。
class Solution {
boolean check(int l, int r, int mid, int[] nums, int target) {
if (nums[l] <= nums[r]) { // 已经在递增区间了,很好判断 mid 在 target 的左边还是右边。
return nums[mid] >= target;
} else { // 区间仍然是旋转数组,mid 和 target 的位置有六种情况,其中三种满足 mid 在 target 的右边。
// mid 和 target 都在左上方,且 mid 在 target 的右边
if (nums[l] <= target && target <= nums[mid]) return true;
// mid 和 target 都在右下方,且 mid 在 target 的右边
if (target <= nums[mid] && nums[mid] <= nums[r]) return true;
// mid 在右下方,target 在左上方,且 mid 在 target 的右边
if (nums[mid] <= nums[r] && nums[l] <= target) return true;
return false;
}
}
public int search(int[] nums, int target) {
// 因为 check 函数的约束,这里我们只搜索除了最后一个元素以外的位置
int l = 0, r = nums.length - 1;
while (l < r) {
int mid = l + (r - l ) / 2;
if (check(l, r, mid, nums, target)) {
r = mid;
} else {
l = mid + 1;
}
}
// 如果没有满足条件的, l 指向 nums[nums.length - 1]
// 如果有满足条件的,l 也可能没有取等
if (nums[l] != target) return -1;
return l;
}
}