2021/04/17
思路
根据中位数的性质,可以把原问题转化为找到一个划分,他把两个数组分别切成左右两个部分,满足性质:
- 左部的元素个数要么跟右部元素个数相同,要么左部多一个元素
- 左部分最大元素小于等于右部分最小元素
如果两个数组的长度之和是奇数,那么左部分的元素个数会比右部分的元素个数多一个,此时中位数为左部分的最大值;否则是做部分的最大值和右部分的最小值的平均数。
定义问题
上面只是描述了思想,下面我们对这个抽象的思想进行形式化的定义。
我们定义 数组 A 的第 i 个划分 为:从数组 A 的下标 i 之前的空隙处划一刀,其中 $i \in [0, \text{len})$
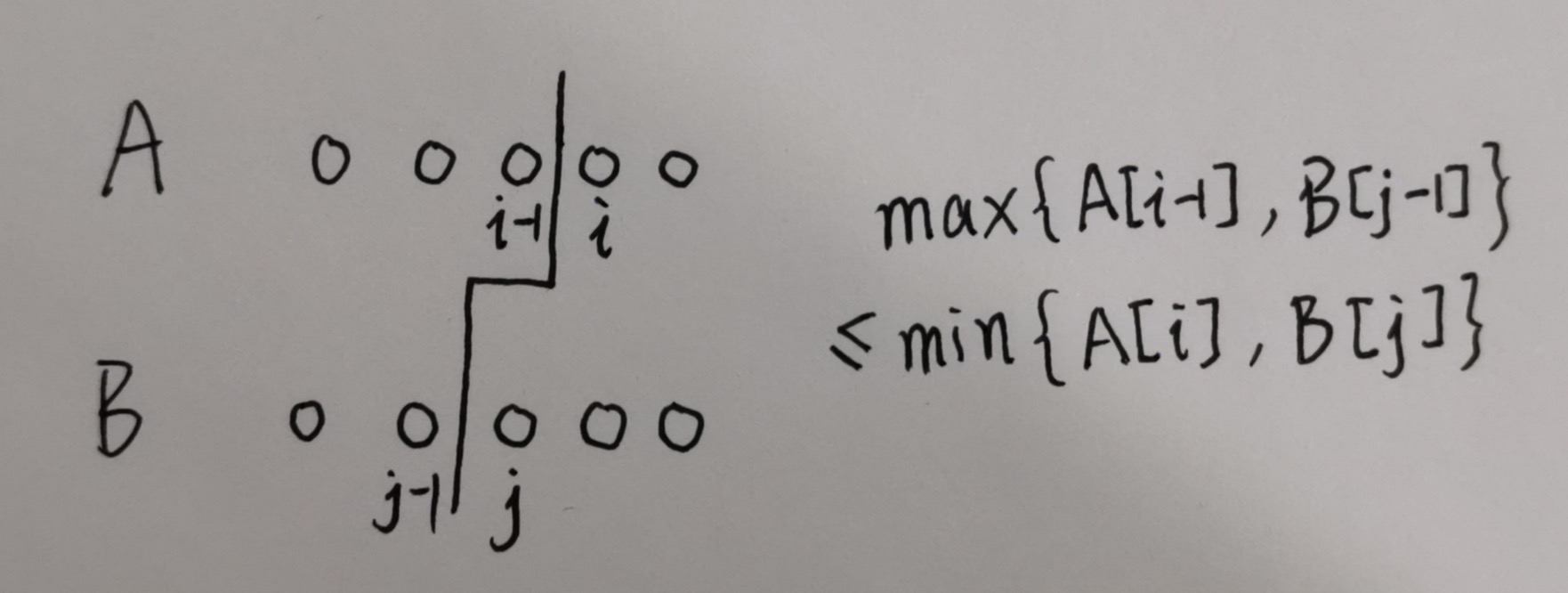
我们要找到的划分是满足性质 A[i-1] <= B[j] && B[j-1] <= A[i] 的划分,但是这个性质只适合遍历搜索使用,满足这个性质的划分可能有多个。 例如:
A: 12221
B: 12221
对于数组A,我们列出所有的划分,满足性质的是中间的三个划分 [F,T,T,T,F]。
可以看到,这个性质不是一个可以用于二分求解的性质,因为它不单调。因此,我们需要把该性质转化为一个可以方便进行二分查找的性质。
转化问题
通过观察上图的数组 A,如果位置 i 是 第一个 满足 A[i] >= B[j-1](意味着 A[i-1] < B[j]),那么位置 i 正是符合要求的划分。
因此,我们定义可二分搜索的性质为:满足 A[i] >= B[j-1] 的划分。
你可以看到,我们事实上通过 减弱命题 的方式,把一个 [F,T,T,T,F] 的暴力搜索问题,变成了 [F,T,T,T,T] 的二分搜索问题。
【注意】:如果最后没有找到满足这个性质的划分,那么也产生了一个划分,数组 A 全部都被划分到了左半部分,此时,左半部分的最大值也是小于右半部分的最小值的,所以这个划分必然是合法的。
代码实现
为了减少一些心智负担,使我们即便过了很久之后,也能把这个算法一次写对。我们先对两个数组进行交换,减少二分区间的起始坐标的计算。 然后就是边界情况处理了,不再赘述。
该实现的二分搜索部分,是一个标准的左闭右开False/True二分模板,不需要过脑袋直接写即可。
use std::mem::swap;
use std::cmp::{max, min};
impl Solution {
pub fn find_median_sorted_arrays(mut nums1: Vec<i32>, mut nums2: Vec<i32>) -> f64 {
if nums1.len() > nums2.len() {
swap(&mut nums1, &mut nums2);
}
return Solution::find_median_sorted_arrays_0(&nums1, &nums2);
}
fn check(a: &Vec<i32>, b: &Vec<i32>, total_left: &usize, mid: usize) -> bool {
let j = total_left - mid;
return a[mid] >= b[j - 1];
}
fn find_median_sorted_arrays_0(a: &Vec<i32>, b: &Vec<i32>) -> f64 {
let total_left = (a.len() + b.len() + 1) / 2;
// 无脑的标准左闭右开二分,返回满足性质的第一个位置
let mut l = 0;
let mut r = a.len();
while l < r {
let mid = l + (r - l) / 2;
if Solution::check(&a, &b, &total_left, mid) {
r = mid;
} else {
l = mid + 1;
}
}
let i = l;
let j = total_left - i;
// 边界处理
let a_left_max = if i == 0 { i32::MIN } else { a[i - 1] };
let a_right_min = if i == a.len() { i32::MAX } else { a[i] };
let b_left_max = if j == 0 { i32::MIN } else { b[j - 1] };
let b_right_min = if j == b.len() { i32::MAX } else { b[j] };
if (a.len() + b.len()) % 2 == 0 {
return (max(a_left_max, b_left_max) + min(a_right_min, b_right_min)) as f64 / 2.0;
} else {
return max(a_left_max, b_left_max) as f64;
}
}
}
转化为 find_kth 问题
用同样的思路,可以实现 find_kth,寻找两个有序数组归并后第 k 个数。
划分的时候,保证左半部分总是有k个元素,并且左半部分的元素小于右半部分的元素。
不过要注意的是,二分的时候不一定能从较短的数组的第0个元素开始切。
use std::mem::swap;
use std::cmp::{max};
impl Solution {
pub fn find_median_sorted_arrays(mut nums1: Vec<i32>, mut nums2: Vec<i32>) -> f64 {
if nums1.len() > nums2.len() {
swap(&mut nums1, &mut nums2);
}
let total = nums1.len() + nums2.len();
if total % 2 == 0 {
let l = Solution::find_kth(&nums1, &nums2, total / 2);
let r = Solution::find_kth(&nums1, &nums2, total / 2 + 1);
return (l + r) as f64 / 2.0;
} else {
return Solution::find_kth(&nums1, &nums2, total / 2 + 1) as f64;
}
}
fn check(short_nums: &Vec<i32>, long_nums: &Vec<i32>, k: &usize, mid: usize) -> bool {
let j = k - mid;
return short_nums[mid] >= long_nums[j - 1];
}
fn find_kth(a: &Vec<i32>, b: &Vec<i32>, k: usize) -> i32 {
// 起始位置计算
let mut l = if k > b.len() { k - b.len() } else { 0 };
let mut r = a.len();
// 标准二分模板
while l < r {
let mid = l + (r - l) / 2;
if Solution::check(&a, &b, &k, mid) {
r = mid;
} else {
l = mid + 1;
}
}
let i = l;
let j = k - i;
// 边界处理
let a_left_max = if i == 0 { i32::MIN } else { a[i - 1] };
let b_left_max = if j == 0 { i32::MIN } else { b[j - 1] };
return max(a_left_max, b_left_max);
}
}