Extracting Top-K Insight 论文实现与解析
2024/07/16
https://acm.sustech.edu.cn/btang/pub/SIGMOD17_insight.pdf
概念
Data Model and Subspace
Dataset
$\mathbb{R}(D,M)$表示一个数据集
- $D=\langle D_1, \dots,D_d \rangle$:维度列表
- $M $:一个度量
- $dom(D_i)$:维度$D_i$的维度成员列表
- $\lvert dom(D_i)\rvert$:维度$D_i$的维度成员数目
subspace
定义:
$S=\langle S[1], \dots,S[d]\rangle$, 其中$S[i]$要么是 $dom(D_i)$里的一个值,要么是 $*$
$*$ 表示该位置可以取所有维度成员的值
$S.M$ 表示对于(子)空间$S$的所有 tuples 进行聚合运算所得的值
这里没有指出是哪种聚合方式,但聚合方式是固定的
举例:
比如我们有一个数据集超市 R(<地区,子类别>,销售额),其中 D = <地区,子类别>,M=销售额
那么 :
- 子空间 S1 = <东北,桌子> 表示:地区为东北,子类别为桌子的所有数据行(tuples)
- 子空间 S2 = <*,桌子> 表示:表示子类别为桌子的所有数据行
- 子空间 S = <*, *> 表示:全体数据
现在我们指定聚合方式为 SUM
- S1.M 表示对子空间 S1 的所有行的销售额进行 SUM 得到的一个值
- S2.M 表示对子空间 S2 的所有行的销售额进行 SUM 得到的一个值
- S.M 表示对子空间 S 的所有行的销售额进行 SUM 得到的一个值
sibling group
定义:
\[\mathrm{\textbf{SG}}(S,D_i)=\{S^{\prime}:S^{\prime}[i] \neq * \land \forall j \neq i,S^{\prime}[j]=S[j]\}\]解释:
sibling group 表示,对于某个子空间 S,使其的第 i 个维度按照 dom(Di) 遍历,可以得到$\lvert dom(D_i)\rvert$个子空间,这些子空间除了第 i 个维度的值不同以外,其它维度位置保持不变。
举例:
SG(<*,桌子>, 地区) = {
<东北,桌子>,
<中南,桌子>,
<华北,桌子>,
<华东,桌子>,
<西南,桌子>,
<西北,桌子>
}
注意:即便地区已经不为 * 了,也可以对这个空间沿着这个维度的维度成员求 sibling group
SG(<东北,桌子>, 地区) = {
<东北,桌子>,
<中南,桌子>,
<华北,桌子>,
<华东,桌子>,
<西南,桌子>,
<西北,桌子>
}
Composite Extractor
extractor
定义:
extractor$\xi $,拿 sibling group $\mathrm{SG}(S,D_x)$作为输入,对于每一个$S_c \in \mathrm{SG}(S,D_x)$,基于
- $S_c.M$
- ${(S_{c’},S_{c’}.M): S_{c’} \in \mathrm{SG}(S,D_x)}$
计算出的 $S_c.M^{\prime}$
论文中列举了几个 Extractor

解释:
extractor 的输入是一串子空间(sibling group),对于 sibling group 中的每一个子空间,根据子空间自己的聚合值,以及 sibling group 中其他子空间的聚合值,根据 extractor 的定义的计算逻辑计算出一个新的聚合值,所以这里是 $S_c.M’$而不是 $S_c.M$,这里可以类比表计算。
举例:
SG(<*,桌子>, 地区) 得到一串子空间,见上一个举例。
<东北,桌子>.M = 100 表示地区为东北,子类别为桌子的销售额是100
<中南,桌子>.M = 110 表示地区为中南,子类别为桌子的销售额是110
<华北,桌子>.M = 120 表示地区为华北,子类别为桌子的销售额是120
<华东,桌子>.M = 130 表示地区为华东,子类别为桌子的销售额是130
<西南,桌子>.M = 140 表示地区为西南,子类别为桌子的销售额是140
<西北,桌子>.M = 150 表示地区为西北,子类别为桌子的销售额是150
比如 Rank Extracor 作用到 SG(<*,桌子>, 地区)
<东北,桌子>.M’ = 6 排名为 6
<中南,桌子>.M’ = 5 排名为 5
…
<西北,桌子>.M’ = 1 排名为 1
Composite extractor
定义:
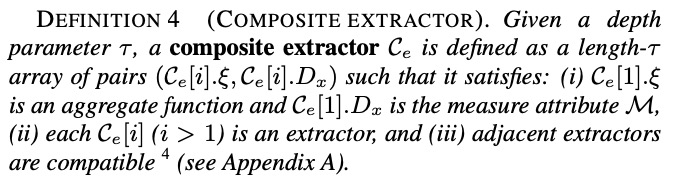

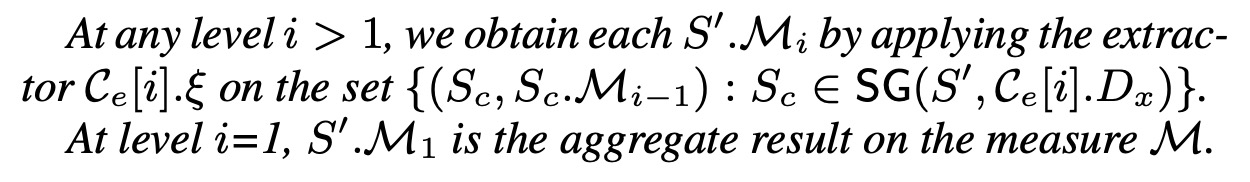
举例:
以论文中的例子举例
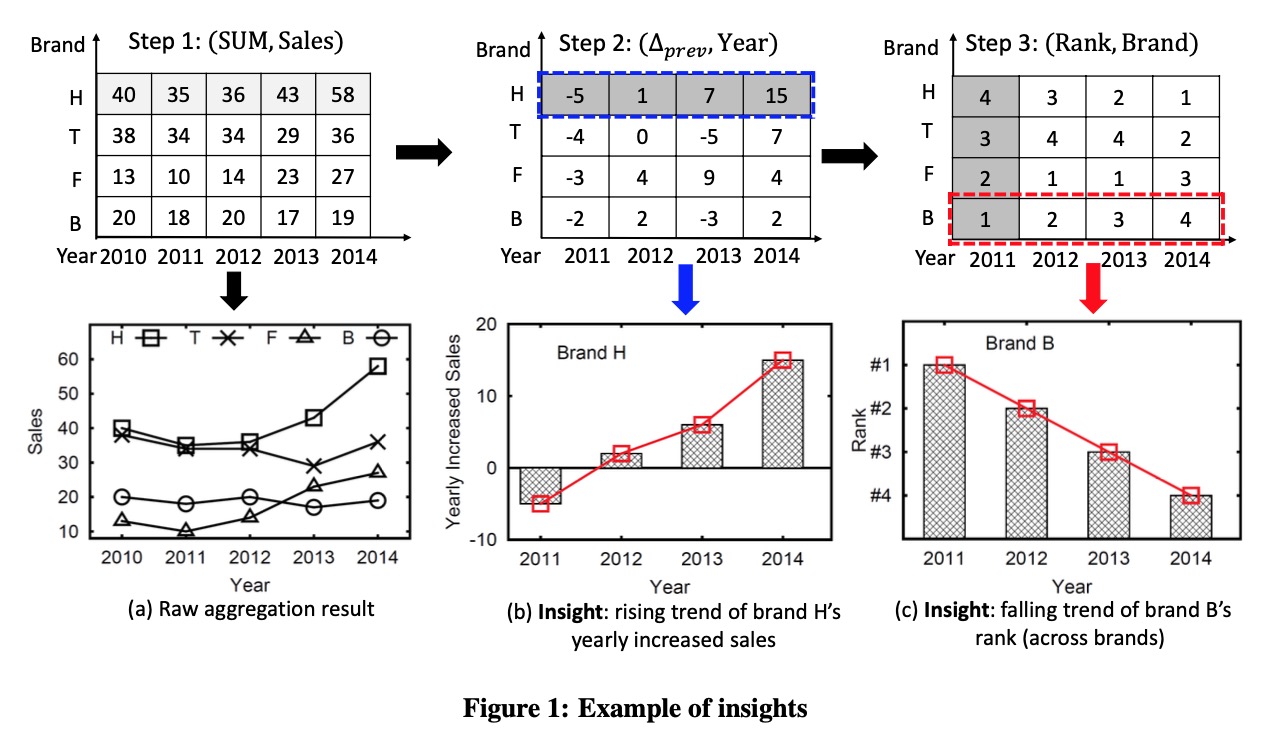
我们令
\[Ce=[(\textrm{SUM},\textrm{Sales}),(\Delta_{prev},\textrm{Year}),(\textrm{Rank},\textrm{Brand})]\]数据集
\[\mathbb{R}(\langle\textrm{Year},\textrm{Brand}\rangle,\textrm{Sales})\]我们将 $Ce$ 作用到 $SG(\langle\textrm{B},*\rangle, \textrm{Year})$ 上,其结果应该为:
\[\Phi=\begin{aligned} \{(\langle \textrm{B},2010\rangle, \langle \textrm{B},2010\rangle.M_3)&, \\ (\langle \textrm{B},2011\rangle,\langle \textrm{B},2011\rangle.M_3)&, \\ (\langle \textrm{B},2012\rangle,\langle \textrm{B},2012\rangle.M_3)&, \\ (\langle \textrm{B},2013\rangle,\langle \textrm{B},2013\rangle.M_3)&, \\ (\langle \textrm{B},2014\rangle,\langle \textrm{B},2014\rangle.M_3)& \} \end{aligned}\]其中 $\langle \textrm{B},2014\rangle.M_3$的计算过程如下:
\[\begin{aligned} \langle\textrm{B},2014\rangle.M_3&=apply \textrm{Rank} on \{(S_c, Sc.M_2):Sc\in \mathrm{SG}(\langle B,2014\rangle,\textrm{Brand})\} \\ &=apply \textrm{Rank} on \begin{aligned} \{(\langle \textrm{H},2014\rangle,\langle \textrm{H},2014\rangle.M_2)&, \\ (\langle \textrm{T},2014\rangle,\langle \textrm{T},2014\rangle.M_2)&, \\ (\langle \textrm{F},2014\rangle,\langle \textrm{F},2014\rangle.M_2)&, \\ (\langle \textrm{B},2014\rangle,\langle \textrm{B},2014\rangle.M_2)& \} \end{aligned} \end{aligned}\]其中 $\langle \textrm{B},2014\rangle.M_2$的计算过程如下:
\[\begin{aligned} \langle \textrm{B},2014\rangle.M_2&= apply \Delta_{prev} on \{(S_c, Sc.M_1):Sc\in \mathrm{SG}(\langle B,2014\rangle,\textrm{Year})\} \\ &=apply \Delta_{prev} on \begin{aligned} \{(\langle \textrm{B},2010\rangle, \langle \textrm{B},2010\rangle.M_1)&, \\ (\langle \textrm{B},2011\rangle,\langle \textrm{B},2011\rangle.M_1)&, \\ (\langle \textrm{B},2012\rangle,\langle \textrm{B},2012\rangle.M_1)&, \\ (\langle \textrm{B},2013\rangle,\langle \textrm{B},2013\rangle.M_1)&, \\ (\langle \textrm{B},2014\rangle,\langle \textrm{B},2014\rangle.M_1)& \} \end{aligned} \\ &=apply \Delta_{prev} on \begin{aligned} \{(\langle \textrm{B},2010\rangle,20)&, \\ (\langle \textrm{B},2011\rangle,18)&, \\ (\langle \textrm{B},2012\rangle,20)&, \\ (\langle \textrm{B},2013\rangle,17)&, \\ (\langle \textrm{B},2014\rangle,19)& \} \end{aligned} \\&=2 \end{aligned}\]同理还可以算出
\[\begin{aligned} \langle \textrm{H},2014\rangle.M_2&=15 \\ \langle \textrm{T},2014\rangle.M_2&=7 \\ \langle \textrm{F},2014\rangle.M_2&=4 \end{aligned}\]所以
\[\begin{aligned} \langle\textrm{B},2014\rangle.M_3 &= apply \textrm{Rank} on \begin{aligned} \{(\langle \textrm{H},2014\rangle,\langle \textrm{H},2014\rangle.M_2)&, \\ (\langle \textrm{T},2014\rangle,\langle \textrm{T},2014\rangle.M_2)&, \\ (\langle \textrm{F},2014\rangle,\langle \textrm{F},2014\rangle.M_2)&, \\ (\langle \textrm{B},2014\rangle,\langle \textrm{B},2014\rangle.M_2)& \} \end{aligned} \\&= apply \textrm{Rank} on \begin{aligned} \{(\langle \textrm{H},2014\rangle,15)&, \\ (\langle \textrm{T},2014\rangle,7)&, \\ (\langle \textrm{F},2014\rangle,4)&, \\ (\langle \textrm{B},2014\rangle,2)& \} \end{aligned} \\&=4 \end{aligned}\]同理还可以算出
\[\begin{aligned} \langle \textrm{B},2010\rangle.M_3&=nil \\ \langle \textrm{B},2011\rangle.M_3&=1 \\ \langle \textrm{B},2012\rangle.M_3&=2 \\ \langle \textrm{B},2013\rangle.M_3&=3 \end{aligned}\]所以
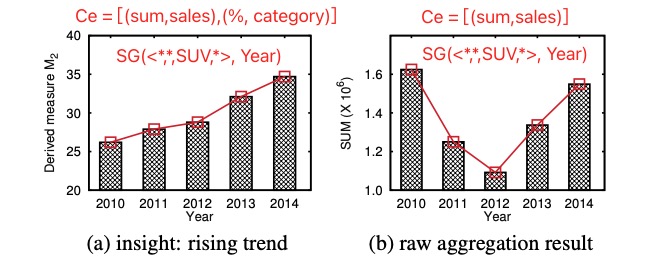
\[\Phi=\begin{aligned} \{(\langle \textrm{B},2010\rangle,nil)&, \\ (\langle \textrm{B},2011\rangle,1)&, \\ (\langle \textrm{B},2012\rangle,2)&, \\ (\langle \textrm{B},2013\rangle,3)&, \\ (\langle \textrm{B},2014\rangle,4)& \} \end{aligned}\]这就得到了论文引言例子里第二个 Insight
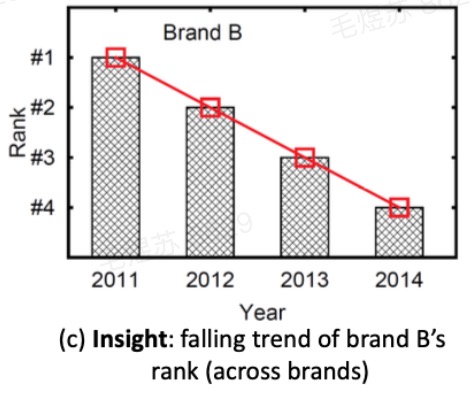
事实上,在这个数据集上,我们使用 Rank 和 ΔPrev 这两个 extractor,还可以算出如下结果,箭头所指部分就是上图所示的 Insight
0.07419 [(Sum,Sales),(Δprev,Year),(Rank,Brand)] SG(<H,*>,Year) => ,4,3,2,1
0.04899 [(Sum,Sales),(Δprev,Year),(Rank,Brand)] SG(<*,2014>,Brand) => 1,2,3,4
0.03395 [(Sum,Sales),(Δprev,Year),(Rank,Brand)] SG(<*,2011>,Brand) => 4,3,2,1
0.03290 [(Sum,Sales),(Δprev,Year),(Rank,Brand)] SG(<B,*>,Year) => ,1,2,3,4 <======
0.00662 [(Sum,Sales),(Δprev,Year),(Rank,Brand)] SG(<*,2012>,Brand) => 3,4,1,2
0.00124 [(Sum,Sales),(Δprev,Year),(Rank,Brand)] SG(<T,*>,Year) => ,3,4,4,2
0.00063 [(Sum,Sales),(Δprev,Year),(Rank,Brand)] SG(<F,*>,Year) => ,2,1,1,3
0.00000 [(Sum,Sales),(Δprev,Year),(Rank,Brand)] SG(<*,2013>,Brand) => 2,4,1,3
0.00000 [(Sum,Sales),(Δprev,Year),(Rank,Brand)] SG(<*,2010>,Brand) => ,,,
Insight Problem
首先形式化的描述要解决的问题是什么:
定义:

解释:
对于一个数据集的所有的 $\mathrm{SG}(S,D_i)$,把所有可能的 Composite Extractor 应用到这个 sibling group 后,都可以得到一个 $\Phi$,然后我们根据 Insight Type $\mathrm{T}$的不同,用不同的打分函数给这个$\Phi$打分,得分前 K 高的组合 ${(\mathrm{SG}(S,D_i),C_e,\mathrm{T})}$,就是我们寻找的 Insight 集合。
论文的正文给出了两种类型的 Insight(附录给了 corelation 类型的 Insight):

所以这个问题如何解决,伪代码就可以先写出来了:
let TopKInsight = new TopKSet(k);
function findTopKInsight() {
let allCompositeExtractors = generateCes(depth); // depth 为 2 或 3
for (let ce of allCompositeExtractors) {
for (let di of dimensions) {
// 遍历数据集 S 的所有可能的 siblingGroup,把 ce 应用上去得到一个 ϕ
dfs(S, di, ce);
}
}
}
// 输入是 SG(S,di) 和 ce
function dfs(S, di, ce) {
// 对于所有可能的 SG(S,di)
let sg = siblingGroup(S, di);
// 把 ce 应用到这个 sg,这个函数是递归函数
let ϕ = extract(sg, ce);
// 计算不同 Insight 类型的分数
for (let T of InsightTypes) {
// 用不同的打分函数给这个结果集打分
let score = calcScore(ϕ, T);
// 如果该分数是当前的 topK 就存下来
if (TopKInsight.isTopKScore(score)) {
TopKInsight.add({sg, ce, T, score, ϕ});
}
}
// 继续向下遍历其它子空间
for (let subspace of sg) {
for (let d of dimensions) {
if (subspace.attr(d) === '*') {
dfs(subspace, d, ce);
}
}
}
}
Insight Score Function
Score 的定义:
\[\mathbb{S}(\mathrm{SG}(S, Di ), Ce , \mathrm{T}) = \mathrm{\textbf{Imp}}(\mathrm{SG}(S, Di )) \cdot \mathrm{\textbf{Sig}}_T (Φ)\]Imp(Impact)的定义:
\[\mathrm{\textbf{Imp}}(\mathrm{SG}(S,Di))=\frac{\sum_{S'\in SG(S,Di)}\mathrm{SUM}(S')}{\mathrm{SUM}(⟨∗, · · · , ∗⟩)}\]Sig(Significance)的定义:
To achieve generality, we measure the p-value of different types of insights by using different kinds of null hypotheses
解释:
- Imp 表示一个 sibling group 的该度量在全体空间中的占有率,他只跟空间本身的性质有关,与 Insight 的类型无关。比如 SG(<,桌子>, 地区) 的SUM(销售额)比 SG(<,铅笔>, 地区)的SUM(销售额)要高,那么前者的 Imp 分数就较高。
- Sig 跟 Insight Type 有关,采用了数理统计的假设检验中的p值检验,需要构造一个零假设(null hypotheses),p值越大,则零假设越显著,所以 Imp 一般可设为 1 - p。之所以用p值检验,是为了让不同的 Insight 的分数是可比较的。
- Imp 和 Sig 的取值范围都是 0~1。
系统架构
总览:
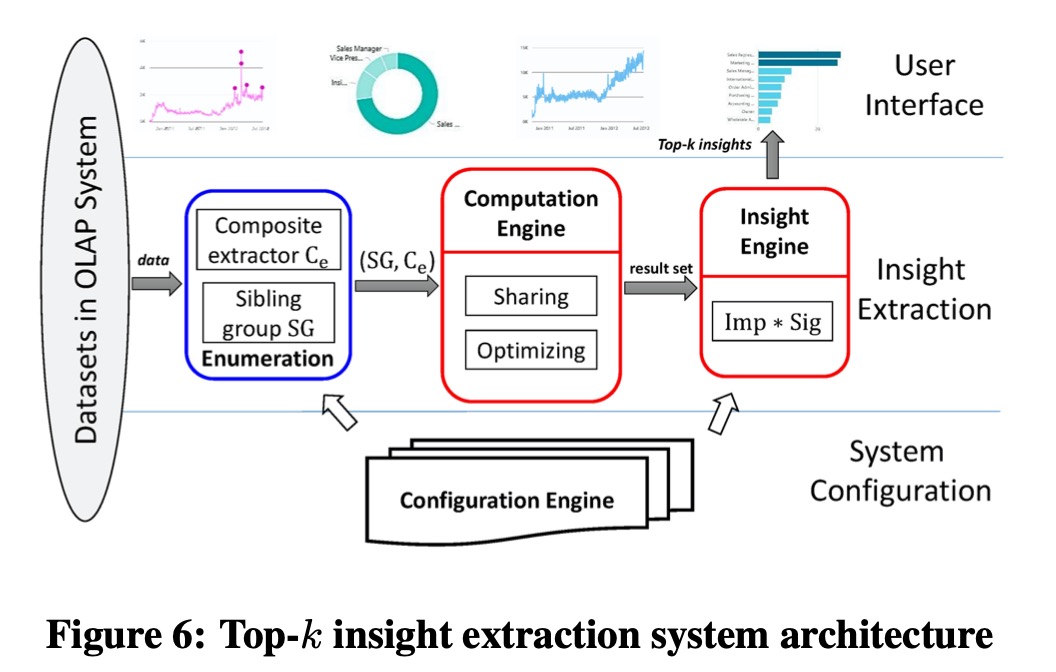
可拓展性:
- 聚合方式可扩展
- Extractors 可扩展
- 度量不仅支持原始字段,也支持计算字段
- Insight 的类型可扩展,Insight 的打分函数可定制
- 搜索空间可由用户指定,用户可以指定他感兴趣的子空间
算法流程
EKI


Algorithm 1 基本上就是上面给出的 js 伪代码
EKI 算法只使用了一个优化策略:data cube
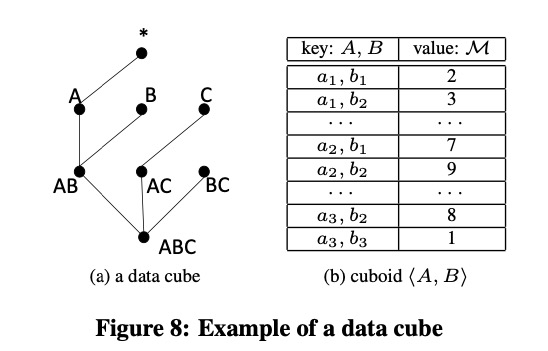
EKIO
可以看到,其实这个算法就是一个 DFS,那么想要提高算法的效率,首先想到的一个办法就是剪枝。论文的第六章给出了剪枝的技术。
Upper Bound Score
因为在某个 siblingGroup 上跑 Ce,得到的结果的分数是 Imp * Sig,这两者都是大于 0 小于 1 的数字,所以 Imp * Sig <= Imp。而 Imp 又只跟空间自身的性质有关,跟具体的 extractor 和应用结果无关,所以我们可以定义一个 Upper Bound Score:
\[\mathrm{\textbf{Imp}}(S)=\mathbb{S}^{UB}(\mathrm{SG}(S, Di ), Ce , \mathrm{T})\geq\mathrm{\textbf{Imp}}(\mathrm{SG}(S, Di )) \cdot \mathrm{\textbf{Sig}}_T (Φ)\]所以我们在把 Ce 应用到 SG 之前,可以预先知道所得分数的上限,如果这个上限都已经不能进入前 K,就可以跳过这个 SG,减少运算量。
Subspace Ordering

Dfs 的时候,如果我们能先遍历 Imp 比较大的空间,这样就更有可能让分数属于前 k 的结果被提前收集,后面空间得分比较小的空间,就更可能被跳过了,从而实现了剪枝。
Sibling Cube
作者发明了一个叫 Sibling Cube 的数据结构(别的地方没有搜到这个名字),来替换 EKI 中的 data cube。
定义:

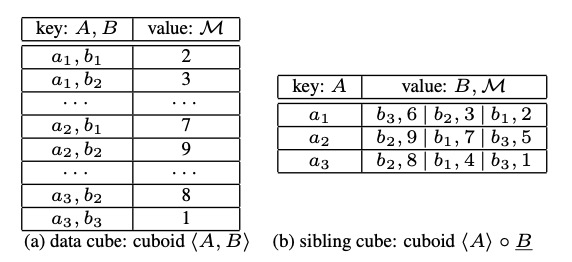
解释:
首先,不管是 data cube 还是 sibling cube ,一个 cube 都是由很多 cuboid 组成的,每一个 cuboid 又是由很多 cube cell 组成的。
对于 sibling cube 中的一个 cuboid
\[\langle D_{k_1},\cdots,D_{k_m}\rangle \circ D_{k_s}, \forall j\in[1,m] k_s\neq k_j\]里面的每个 cell 的 key 为 $\langle D_{k_1},\dots,D_{k_m}\rangle$的维度成员的一个排列,value 是滑动$D_{k_s}$的维度成员,与前一个排列构成了一个子空间数组(每个子空间满足除了上面 m+1 个维度外,其它维度都是 *),每个子空间SUM聚合可以得到一个值,然后按 SUM 从大到小排列。
(这里如果聚合方式不是sum,sibling group 也应该按 sum 从大到小排列)
使用 sibling group 后:
- subspace ordering 优化可以自然而然的得到,不需要额外的排序操作。
- 减少了hash table lookup 次数
缺点是 sibling group 占用的空间比 data cube 要大,作者说可以用 iceberg cube technique 去显著减少 cube size,使之能够被存储在内存中,需要学习一篇 1999 年的论文:
Bottom-up computation of sparse and iceberg cubes.pdf
这个 cube 优化技术我还没有研究,没有实现。
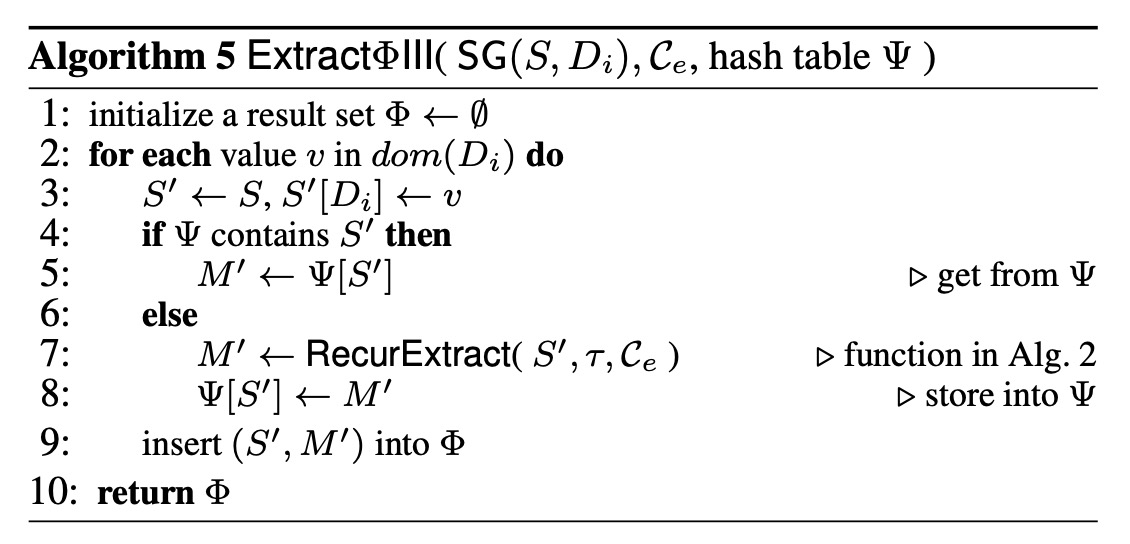
举例:
data cube:

sibling cube:

EKISO
论文的第七章介绍了,如何提高 Extract 的计算效率(COMPUTATION SHARING),这里不详细介绍了,论文附录也给出了伪代码。我基本上用 js 实现了
论文伪代码总览
EKI:Algorithm 1 + Algorithm 2
EKIO:Algorithm 3 + Algorithm 2(slibling cube 版)
EKISO:Algorithm 6 + Algorithm 4 + Algorithm 5,
其中 Algorithm 5 使用到了 Algorithm 2(slibling cube 版)





算法性能研究
机器配置:Intel i7-3770 3.4GHz processor, 16GB of memory
编程语言:C#
真实数据集(Tablet sales)
这份数据是商业数据,不公开,论文没有提数据规模,只是为了显示出,EKISO 的性能很快,而 EKI 不太可用。
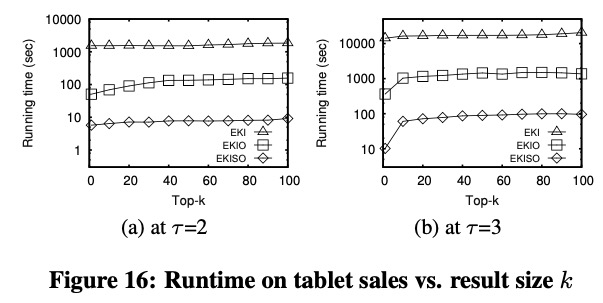
标准数据集(TPC-H)
使用 tpc-h 数据集的 lineitem 表,取100万行
维度和维度成员个数如下:
l_shipdate(2526)
l_discount(11)
l_returnf lag(3)
l_shipinstruct(7)
l_shipmode(4)
l_linestates(2)

测试结果如下:
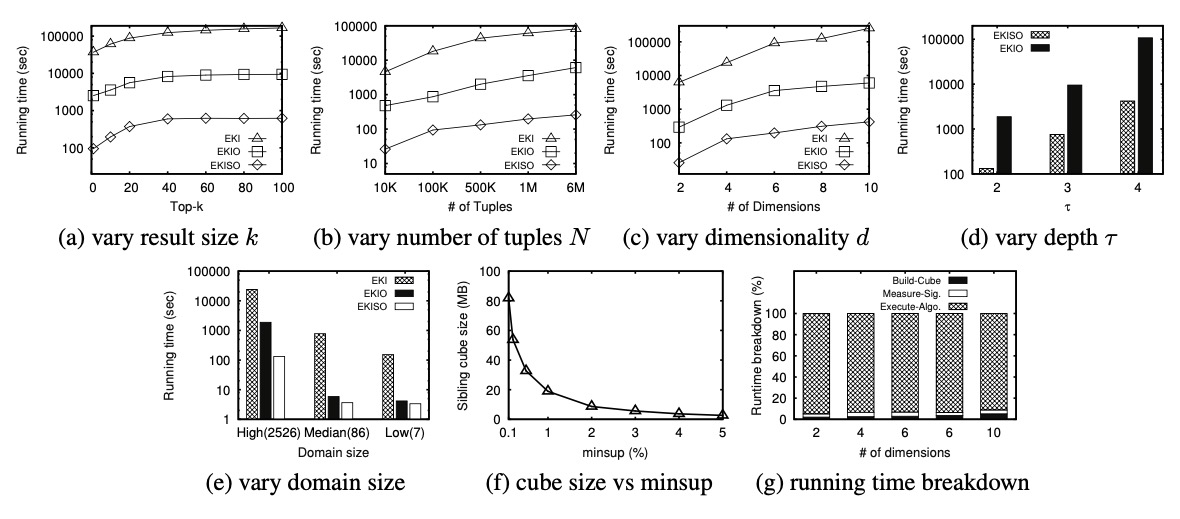
有效性研究
实用性研究
对某公司内部的一个数据集进行了计算,采访了三个经理和三个数据分析师,让他们对生成的洞察的有效性和难度(相对于使用 Excel 透视表复现的难度)进行打分
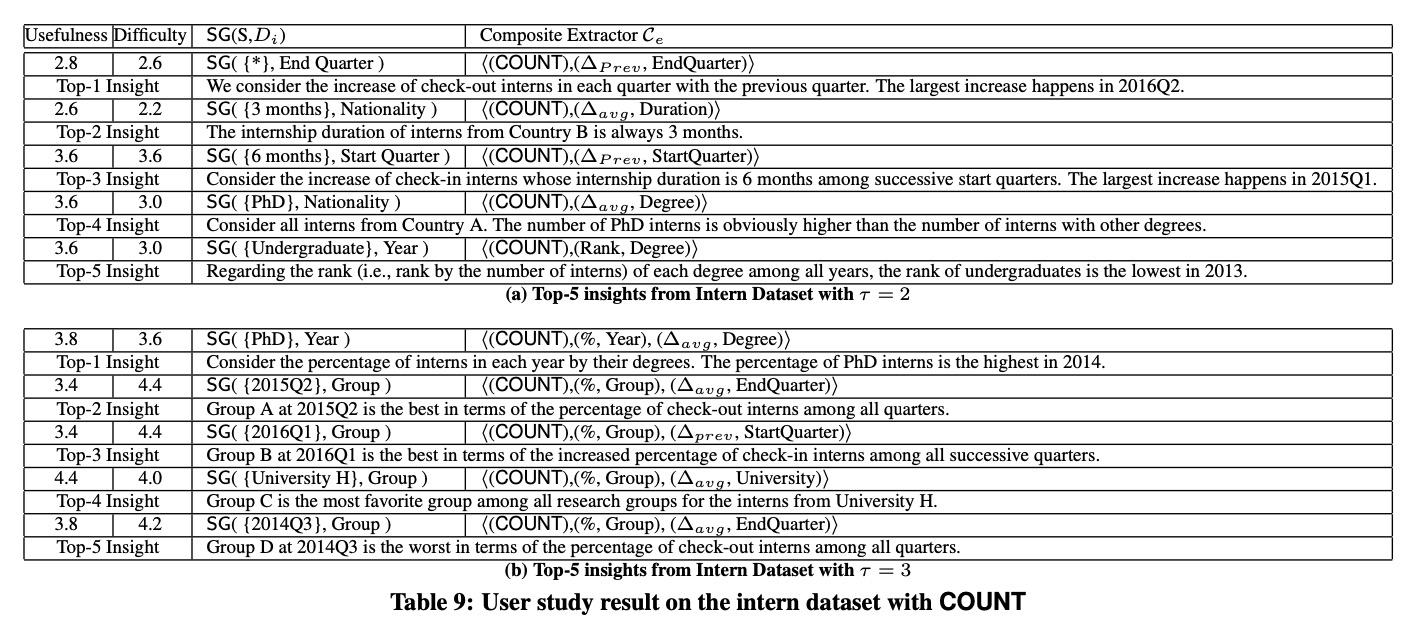
打分的结果显示,二阶洞察的有效性小于三阶洞察,三阶洞察的实现难度比二阶高。
人力研究
找了个数据集,给出了一个二阶洞察,让四个资深数据库研究者,分别用 SQL 和 Excel 透视表复现这个洞察,下面是耗时情况(单位分钟)。

算法只需要 0.17秒
如何与传统 BI 相结合
图表恢复:Insight => 图表
举例
我们以论文引言里的数据集作为例子:
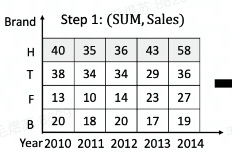
可以跑出如下的 Insight
[depth = 2]
0.91005 [(Sum,Sales),(Δprev,Year)] SG(<*,*>,Year) => ,-14,7,8,28
0.34454 [(Sum,Sales),(Δprev,Year)] SG(<H,*>,Year) => ,-5,1,7,15
0.17957 [(Sum,Sales),(Δprev,Year)] SG(<T,*>,Year) => ,-4,0,-5,7
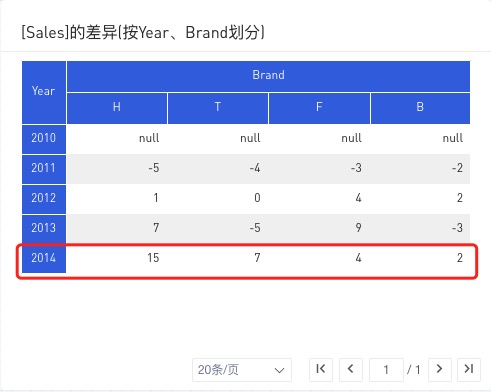
0.17014 [(Sum,Sales),(Δprev,Year)] SG(<*,2014>,Brand) => 15,7,4,2 <======
0.09529 [(Sum,Sales),(Rank,Brand)] SG(<*,*>,Brand) => 1,2,4,3
0.06093 [(Sum,Sales),(Rank,Year)] SG(<*,*>,Year) => 3,5,4,2,1
0.04899 [(Sum,Sales),(Rank,Brand)] SG(<*,2014>,Brand) => 1,2,3,4
0.03920 [(Sum,Sales),(Rank,Brand)] SG(<*,2013>,Brand) => 1,2,3,4
0.03836 [(Sum,Sales),(Δprev,Year)] SG(<F,*>,Year) => ,-3,4,9,4
0.03395 [(Sum,Sales),(Δprev,Year)] SG(<*,2011>,Brand) => -5,-4,-3,-2
[depth = 3]
0.19738 [(Sum,Sales),(Δprev,Year),(Rank,Year)] SG(<*,*>,Year) => ,4,3,2,1
0.12034 [(Sum,Sales),(Δprev,Year),(Δprev,Year)] SG(<F,*>,Year) => ,,7,5,-5
0.11802 [(Sum,Sales),(Rank,Year),(Δprev,Year)] SG(<T,*>,Year) => ,2,0,2,-3
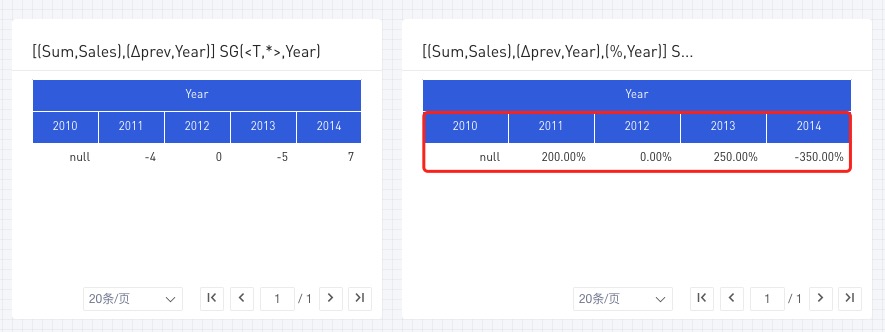
0.11651 [(Sum,Sales),(Δprev,Year),(%,Year)] SG(<T,*>,Year) => ,2,0,2.5,-3.5 <======
0.10965 [(Sum,Sales),(Rank,Year),(Δprev,Year)] SG(<*,*>,Year) => ,2,-1,-2,-1
0.08378 [(Sum,Sales),(Rank,Brand),(Δprev,Year)] SG(<*,2013>,Brand) => 0,0,-1,1
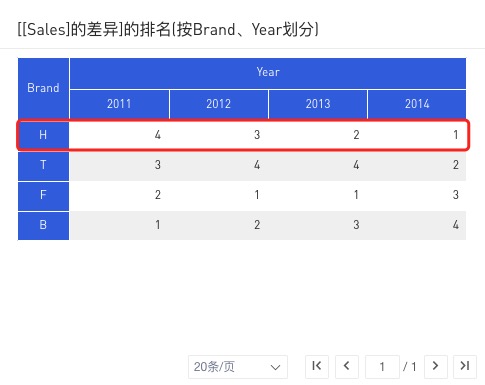
0.07419 [(Sum,Sales),(Δprev,Year),(Rank,Brand)] SG(<H,*>,Year) => ,4,3,2,1 <======
0.07419 [(Sum,Sales),(Δprev,Year),(Rank,Year)] SG(<H,*>,Year) => ,4,3,2,1
0.05564 [(Sum,Sales),(Δprev,Year),(Δprev,Year)] SG(<H,*>,Year) => ,,6,6,8
0.05428 [(Sum,Sales),(Δprev,Year),(%,Year)] SG(<*,*>,Year) => ,-0.4827586206896552,0.2413793103448276,0.27586206896551724,0.9655172413793104
以 [(Sum,Sales),(Δprev,Year)] SG(<*,2014>,Brand) => 15,7,4,2举例:
以 [(Sum,Sales),(Δprev,Year),(Rank,Brand)] SG(<H,*>,Year) ,4,3,2,1 举例:
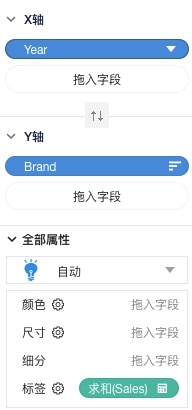
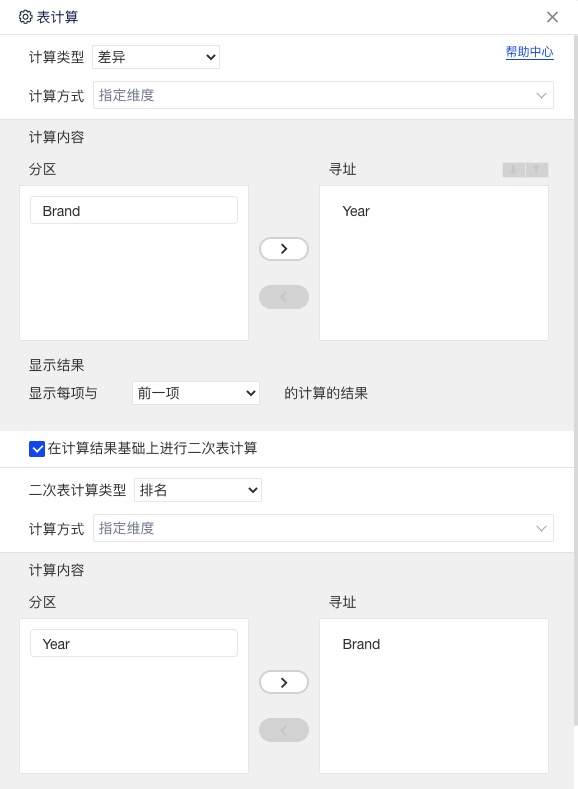
以[(Sum,Sales),(Δprev,Year),(%,Year)] SG(<T,*>,Year) => ,2,0,2.5,-3.5举例:
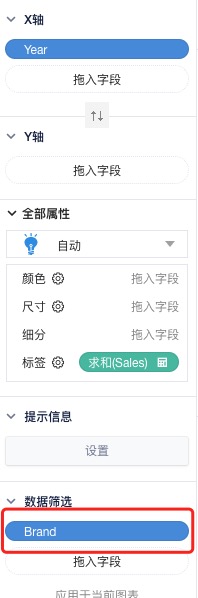
待继续研究的问题
- 洞察值的图表推荐(比如总额百分比可以考虑用斌图,趋势类可以考虑用折线图或柱状图等)
- 洞察类型的扩充
- Extractor (或表计算)衔接的合理性,比如差异后面接总额百分比不一定有意义
数据解释
业界现状
业界已经在增强分析方向做出了产品(字节飞书机器人 & 阿里钉钉机器人)


https://powerbi.microsoft.com/en-us/
https://powerbi.microsoft.com/en-us/blog/announcing-power-bi-integration-with-cortana-and-new-ways-to-quickly-find-insights-in-your-data/
实现数据解释的方案
问题:解释 为什么 2022 的销售额相比 2021 年下降了 101 万
方案:构造一个 Composit Extractor
\[Ce=[(\textrm{SUM},\textrm{Sales}),(\Delta_{prev},\textrm{Year})] \text{ apply on }\mathrm{SG}(S', \mathrm{Year}) \forall S'\in \langle*,*,\cdots,*\rangle\]score function 可以取 $\frac{-\Delta_{prev}}{\color{red}101万}$的值(对下降值的占比越高,贡献越显著)
我们跑出来的结果集
<*, *> -101万
<中南, *> -64万 | <*, 文具> -63万
<中南, 文具> -60万
优势:
不需要用户自己下钻探索,瞬间展示所有可能的下钻粒度中,最有意义的前 k 个结果。